In this tutorial I will explain how to create DEM and also creating elevation profile in QGIS. There were some questions arose about it after my last post with the title how to create contour line in QGIS. I'd like to write this topic sometimes ago, but just not having time to do it. Finally I could sit in a rainy afternoon and started writing this tutorial for you.
I started this post with a question: How to create elevation profile in QGIS using contour line? I tried to answer the question and found that the elevation profile can't be created right away using contour line in QGIS, but using DEM. Therefore we have to create a DEM first and then an elevation profile can be created using the DEM data. So let's see how to do it in this tutorial. Anyway for this tutorial I'm using QGIS 3.2 Bonn.
How Create DEM in QGIS
Creating DEM in QGIS using height point data is quite straight forward by using Natural neighbour tool from SAGA. The following steps will guide you how to do that using the tool.
1. Add elevation points data to QGIS as in figure 1.
 | ||||
| Figure 1. Elevation Points Data |
2. Open Natural neighbour tool. The tool can be found in the processing toolbox. In the search field, just type Natural, the tool will be shown under SAGA as in figure 2.
 |
| Figure 2. Natural neighbour tool |
3. After opening the tool, a window as in figure 3 will appear. In this window we setup some parameters such as attribute for height value, method, output extent, cell size, etc. As in figure 3, can be seen that I had setup some those parameters. You can change the parameter for yours.
 |
| Figure 3. Natural neighbour window |
4. After running the Natural neigbour tool by clicking the Run button. It will take sometimes, depends on the number of points. After finished, the DEM will be added to QGIS map canvas as in figure 4.
 | |
| Figure 4. DEM Data |
Congratulation! We just made a DEM using elevation point data in QGIS. Next let's create elevation profile.
How to Create Elevation Profile in QGIS
To create an elevation profile in QGIS, we are using Profile Tool plugin which is developed by Borys Jurgiel and friends. If you don't have it, just install it using menu Plugins >> Manage and Install Plugins. In the plugins window, type Profile. The Profile tool will be appeared as in figure 5.
 |
| Figure 5. Installing Profile Tool Plugin |
To create an elevation profile using Profile tool plugin can be done with several steps as follow:
1. Open Profile tool plugin. The profile tool window will appear as in figure 6.
 |
| Figure 6. Profile tool window |
2. Add the DEM layer using Add Layer button. Then in the selection options select Temporary polyline, because we will draw a temporary polyline on the QGIS map canvas to create an elevation profile for the line,
3. Next, just draw a polyline on the QGIS map canvas where you want to create elevation profile as in figure 7. We can draw a polyline in cross cursor. If you cursor pointer is not in cross type, activate it by clicking the Profile tool icon. To finish a polyline drawing, just double click left mouse button.
 |
| Figure 7. Drawing Polyline |
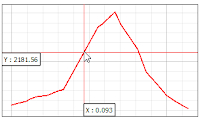
4. When finished the elevation profile will be appeared in the Profile tool window as in figure 8. Move the cursor on the profile, the location of the cursor on the profile also connected with the line on qgis map canvas. So we can see the cursor's position and it's location on the map.
 |
| Figure 8. Elevation Profile |
The profile graph can be saved as image by using Save as button. Furthermore we can also toggle the profile graph into slope mode both in % or degree unit as in figure 9.
That's all the tutorial how to create DEM and elevation profile in QGIS 3. Hopefully it is useful for you and can answer the question above. Once again for the conclusion. An elevation profile can not be constructed right away from contour line, must be in DEM. So we need to create a DEM from elevation point dataset and then create a profile using Profile tool plugin. If you are interested how to create elevation profile with PyQGIS check out this tutorial How to Create Elevation Profile with Python and QGIS. Furthermore might be you want to calculate volume of a DEM. If you do so, please check out this tutorial How to Calculate Raster Surface Volume in QGIS.
Watch the video below to see this tutorial in action
 |
| Figure 9. Slope profile |
Watch the video below to see this tutorial in action
